UNSW High Schools Programming Competition 2017: Open Round
The Tasks: Junior task: Fitness Friend (easy, 7 marks)Task 1. Isomorphic Word Pairs (easy, 7 marks)Task 2. Rats (easy to moderate, 9 marks)Task 3. Queue Jumpers (easy to moderate, 10 marks)Task 4. Inheritance (moderate, 14 marks)Task 5. Connect-4 (moderate to hard, 20 marks)Task J. Fitness Friend Available Marks: 7Smart watches now provide heart rate, walking speed, energy consumption, step counters and sometimes even the time. Everyone knows they should try to walk a certain minimum number of steps each day, and watches will often set a new target daily based on the number of steps taken over the last few days and the current target. Fitness Friend, ProgComp's proposed software that will only get to market if you can implement it for us, goes one step (sorry) further. Some people are discouraged if they keep failing to reach their target: they have low motivation. Others try to outdo themselves every day and want an always-increasing target: they're highly motivated. Fitness Friend introduces a self-nominated motivation factor M, an integer between 0 and 100. The way it works is shown in the diagram below. 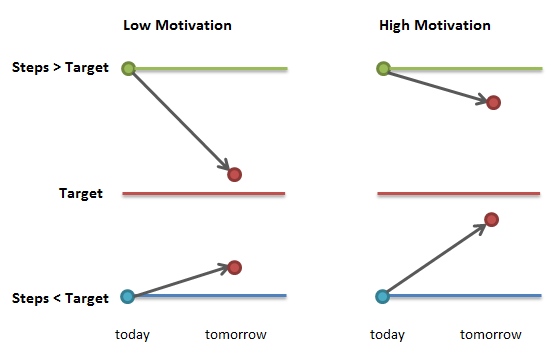 The new-target calculation is given by two similar formulas, depending on whether today's target was reached: 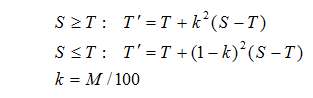 For example, if M is 45, T is 7500 and S is 7125, the second formula gives k = 0.45, (1–k)2 = 0.55*0.55 = 0.3025, which you round down to 7386.T ′ = 7500 + 0.3025 * (7125 – 7500) = 7500 + 0.3025 * (–375) = 7500 – 113.4375 = 7386.5625 Your taskWrite a program that calculates the daily targets given motivation and daily step counts, collecting simple statistics to report at the end. The first line of input has the Motivation Factor and starting target, separated by a space. The rest of the input has the daily steps, one per line. A negative value ends the list (and isn't counted as step data of course). Your program should list all the targets on one line, then on a new line show
Example80 7500 8231 7700 9015 6000 -1produces... 7500 7967 7956 8633 8527 Motivation 80, days 4, mean steps 7736, goal reached 50%. Final target 8527If the same step data is used but the motivation is changed from 80 to 30, the targets are more modest and the goal is reached more easily: 7500 7565 7577 7706 6870 Motivation 30, days 4, mean steps 7736, goal reached 75%. Final target 6870 Test dataTest your program using the following data. 60 8200 8350 10245 9254 7957 7880 7885 8194 8114 10176 9625 8492 9550 9483 10498 10511 9033 9215 10655 9791 8210 10664 8251 9800 8310 9614 7682 9327 7785 10527 9881 -1 Bonus PointsSimple programs can sometimes be used as tools to analyse aspects of the problem area. In this case there's an interesting relationship between motivation and the final target, which is monotonic increasing (this just means the greater the motivation, the higher the final target). By changing the motivation in the data file and rerunning the program, you could identify points on the relationship curve, or estimate the motivation required to set a specified target for this data set. Use the program, without changing it at all, to find out what motivation is required to achieve a final target of 9888 for the steps in the test file (888 is an auspicious number in some cultures). Be smart about this, like the watch: try 50, halfway between 0 and 100. if the result is too high try 25 (halfway between 0 and 50), otherwise try 75. Keep going this way, choosing the midpoint between the deduced smallest and largest possible motivation, according to each result. This technique is called binary search, and is an important programming principle. While you're not programming it here, you are applying it to avoid having to try all possibilities. It will give you the answer in no more than 7 tries (log2 100). For bonus points, show each motivation value you tried, the last one being the answer. You get one for the correct answer but two for the binary search technique (if done approximately correctly). Note: bonus points are not included in the qualifying score for the finals, sorry. Assessment
Image source: myelmm.com Task 1. Isomorphic Word Pairs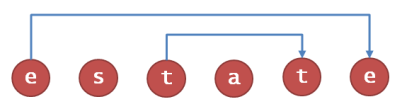 Available Marks: 7Two words are called isomorphs (or more accurately, form an isomorphic pair) if they have the same length and the same pattern of repeated letters. The letters don't need to match between the words, only the positions where the repetitions occur. Isomorphs are of interest because one could be converted to the other using a simple substitution cipher. Consider the words estate and tenant. In both cases the first letter is repeated five places later, and the third letter two places later. Letters in the other positions are not repeated. Define a repetition pattern to be an ordered list of relative positions where each letter is next repeated, with 0 indicating no repetition and a + preceding the repetitions for better readability. Thus both words have the repetition pattern +5 0 +2 0 0 0The same rules apply even if a letter occurs more than twice, so the words cannon and kisses have the pattern 0 0 +1 +2 0 0People who like wordplay look for isomorphic pairs that form an incongruous phrase, like dysfunctional ventriloquism, but that level of semantic analysis is beyond even ProgComp entrants. Your taskWrite a program that identifies whether pairs of words are ismorphs. Input consists of the number of pairs on the first line (maximum 20), and then each pair on subsequent lines, separated by a space. Words are between 1 and 20 letters long, all lower-case, no punctuation. For each pair, your program should list the two words and classify them as either
Example6 secret cowboy yummy tweet exponential amputations reflective programmer financial turnaround cutthroat communismproduces... secret, cowboy are isomorphs with repetition pattern 0 +3 0 0 0 0 yummy, tweet are isomorphs with repetition pattern +4 0 +1 0 0 exponential, amputations are isomorphs with repetition pattern +5 0 0 0 +2 0 0 0 0 0 0 reflective, programmer are not isomorphs financial, turnaround have different lengths cutthroat, communism are isomorphs with repetition pattern 0 0 +1 +5 0 0 0 0 0 Test dataTest your program using the following input. 20 all inn doll door level kayak squeaky sunlamp gutless sheriff trapdoor flywheel mistiest monsoons throwaway hepatitis explosive magnesium wealthiest subterfuge kookaburra toothbrush sportswomen spokeswoman tightfisted hitchhikers cryptography manipulation sharpshooter marshmallows ambidextrous thunderclaps incompatible housewarming sportsmanlike environments disfranchised stepdaughters fastidiousness lasciviousness Source: Programming Puzzles and Code Golf, contributed by user xnor. Task 2. Rats Available Marks: 9RATS (in this context) stands for Reverse, Add, Then Sort, applied to a positive decimal integer. It's the generating algorithm for an integer sequence that either diverges, or enters a reasonably short cycle. Consider the integer 180. Reversing the digits gives 081, or just 81. 180 + 81 = 261. Sorting the digits gives 126. Continuing, 126 + 621 = 747, sorted = 477 477 + 774 = 1251, sorted = 1125 1125 + 5211 = 6336, sorted = 3366 3366 + 6633 = 9999, sorted = 9999 9999 + 9999 = 19998, sorted = 18999 18999 + 99981 = 118980, sorted = 011889 11889 + 98811 = 110700, sorted = 000117 117 + 711 = 828, sorted = 288 288 + 882 = 1170, sorted = 117So the sequence ends in a cycle of period 2 (the period of a cycle is the number of different values it contains). Only a small number of different cycles can occur, we want to find them. Your taskWrite a program that identifies all cycles that occur for starting numbers less than 10000 (or 1000 for fewer marks). If any sequence element exceeds 1012, you may assume the sequence diverges. Complete answers depend on your computer using 64-bit arithmetic. In the event that your calculations use 32-bit arithmetic and overflow occurs, you will not be penalised provided the other cycles are reported correctly. Your program's output should consist of one cycle on each line, ordered by period and then by the smallest member of the cycle. Each line should show three data items:
Period: 2, occurs 100 times, cycle: 117 288 AssessmentFull marks will be awarded for correctly identifying all cycles and displaying the details according to the requirements. Deductions apply for incorrect identification, or if you don't cover all 9999 starting values, or for not displaying the data in the required order. Reference: Weisstein, Eric W. RATS Sequence. From MathWorld--A Wolfram Web Resource. Image: and bear makes 3. Photographer: Jessica Florence Task 3. Queue Jumpers Available Marks: 10The residents of Q-Town love queuing for the theatre. Some of them also consider particular position numbers to be lucky, so there can be a lot of undignified jostling while waiting in line. The Mayor of Q-Town wants to put a stop to this unseemly behaviour. She decrees that all theatregoers must adhere to the following rules:
On the mayor's signal, everyone re-orders themselves in a dignified way. Those who did not nominate a position are shuffled up or down the queue as needed, maintaining their relative order. Your taskWrite a program to manage Q-Town's orderly queuing system. Input consists of one queuing problem per line, preceded by the number of problems. Each queuing problem consists of the number of patrons, to a maximum of 26, and the position each one would like to occupy. Positions are counted from 1, and 0 means no nomination. People are allocated an upper-case letter in the original queue order, and the solution is the new arrangement of letters representing the revised queue. Assume the data is valid. The program should show both the original order and the final order on separate lines, with a space between each letter. Example3 3 0 0 0 9 9 8 7 6 5 4 3 2 1 5 0 1 5 0 2produces... A B C A B C A B C D E F G H I I H G F E D C B A A B C D E B E A D C Test dataTest your program using the following data. 5 4 4 2 3 1 6 0 0 5 3 4 1 13 0 0 1 2 3 4 5 6 7 8 9 10 11 26 12 13 3 0 15 0 9 10 8 0 0 14 0 2 4 5 0 7 0 11 1 0 0 0 6 0 1 0 Assessment
Image: Microsoft Corp. clipart Task 4. Inheritance Available Marks: 14The system of inheritance that applied to most families with land or a title in England until recent times was called entailment. It was designed to keep the family estate intact as far as possible, by passing ownership to one (generally male) person at a time. Instead of all children, or even just all sons, inheriting the estate on the death of an owner, the eldest surviving son inherits the lot. This rule then applies recursively to his sons. Thus all his male descendents are ahead of his younger brothers, his brothers are ahead of his uncles, and so on. If all male descendents of the original owner are deceased, surviving females are next in line to inherit, but under these conditions:
ExampleThe family tree below shows all the descendents of the original owner, M0. M0 and his eldest son M1 are deceased, and M1's eldest son is the present owner. The numbers in parentheses record the order of inheritance that would apply when M4 dies. 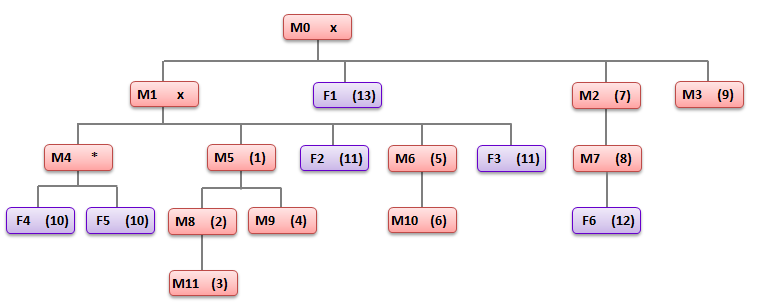 First in line is M4's brother M5 (because M4 has no male heirs), then M5's first son, his grandson, etc. Following all 10 surviving males, the same rules apply to females, starting with M4's daughters, who are jointly 10th in line. In practice males are assigned on a pre-order traversal of the male-line tree and females on a post-order traversal of the male-line tree, which is why F6 inherits ahead of F1. Note that the structure doesn't depend on who's still alive: although dead people can't inherit, their living descendents can. Your taskWrite a program that analyses a family tree and prints the order of inheritance. Input consists of one line for each male, listing his children in descending order of age. The first input line is the number of males. Each person is identified by gender (M or F) and a non-negative integer, unique to that gender. The original owner is always M0, other numbers can be assigned in any order, but without gaps. For each line the patriarch's ID is followed by an optional symbol and a colon, then the IDs of the children. The symbol is either
Output is the present owner and the order of inheritance in one line, separated by spaces. Sample dataThis describes the tree above. It's already sufficiently complex to fully exercise your program. 12 M0x: M1 F1 M2 M3 M1x: M4 M5 F2 M6 F3 M3: M4*: F4 F5 M5: M8 M9 M10: M8: M11 M6: M10 M7: F6 M2: M7 M9: M11:produces... M4 M5 M8 M11 M9 M6 M10 M2 M7 M3 F4+F5 F2+F3 F6 F1 Test dataTest your program using the following two test cases. Test 1: 11 M0*: M3 M6 M1: M5 M2: M1 M3: M4: M10 M2 M5: M6: M7 M9 M7: M8: M9: M8 M4 M10: Test 2: 17 M0x: M3 M14 M11 M4: M8x: F2 M4 M15 M5 M12: M8 M10 M16: M5: M14x: F3 M12 F5 M3*: M9: M6: M13 F4 M10: M9 M6 M2 M2x: M13x: M11: M16 F1 M1 M1: M15: M7 M7: Assessment
Reference: Background information and example are from Image: talentenbank Task 5. Connect-4 Available Marks: 20The Connect-4 game board consists of 7 vertical slots or columns, numbered from 0 to 6, each of which can accommodate up to 6 tokens. Two players take turns to place a token in a slot, we're calling them Red and Yellow. The winner is the first player who has 4 of their tokens in a line, horizontally, vertically or diagonally. Although the game can be fully solved with enough effort, a fair-to-average player can be simulated by scoring possible game positions and looking only a couple of plies ahead (a ply is an action by one player, two plies make up a move). The scoring system assigns points to each sequence of a player's tokens that have a reasonable chance of becoming a winning line. The scoring system to use for this task is as follows: 
The board is represented by 7 fixed-length strings, one for each vertical slot or column. This format best suits operations such as temporarily adding or removing a token, used in game play. Each character is a token (R or Y) or an empty position (a dot). Every legal board column thus begins with zero or more tokens, then empty symbols to make up 6 characters. You can use a different internal representation of course, but input/output uses this format. Consider the following board: RR.... ...... YRRYR. YYR... RYYR.. RYY... Y.....It scores 37 for player R (majority in col 2, pair in col 0, pair in row 2 and a diagonal line of three producing a triple at one end and a PWP at the other). For player Y the same board scores 44 (centre col majority, pair in col 5, triple on row 1, two diagonal triples in one direction and one in the other). Your taskWrite a program that can read boards and score them for a designated player, and for full marks, can also play a full game against a player using a limited strategy. Input consists of board layouts preceded by a line containing score and either R or Y. A line containing the word end terminates the input. Output is a copy of the board in the same format (so we know you've read it properly) and the nominated player and calculated score on the next line. If you were scoring R for the above layout the output would be RR.... ...... YRRYR. YYR... RYYR.. RYY... Y..... Player R scores 37 To play the game (say after processing the normal input), use the following strategy exactly:
R..... Y..... YRRY.. YYRY.. RYR... R..... Y..... Move 9: scores 48-29, 34-40, 47-29, 45-29, 54-20, 37-37, 45-26 R selects column 4 Reply score 20 Y selects column 5 R..... Y..... YRRY.. YYRY.. RYRR.. RY.... Y..... Test dataTest your program using the following data. score Y ...... YRR... YY.... YRR... RRR... YYY... RRY... score R ...... YR.... RYR... YYRRY. YRYYY. RRY... RRY... score Y RYRYY. RYY... RRRYR. YRY... RYRY.. R..... RRR... score R RRYRYY YRY... YRRRYR RYRY.. YRYRY. ...... RRR... score Y YRYRY. RYRYR. YRYRY. YRYRYR RRYRR. Y..... RY.... score R RYRY.. YRYR.. YRR... RYYR.. RYY... YRYR.. RYRY.. end Assessment
Image source: wikimedia |
|
|
